問題概要
$\{1,2,\ldots ,N\}$の部分集合の組$(S_1,S_2,\ldots ,S_k)$について, 以下の条件を満たすものがあれば構築せよ.
- $1,2,\ldots ,N$のうちどの整数も, $S_1,S_2,\ldots ,S_k$のうちちょうど2つに含まれる.
- $S_1,S_2,\ldots ,S_k$のうちどの2つの集合をとっても, その共通成分はちょうど1つである.
制約
- $1\leq N\leq 10^{5}$
考察
とりあえず, $N=1$について考えてみると, $S_1=S_2=\{1\}$として構築できる.
この$S_1,S_2$と共通成分を1つずつもつような$S_3$を作りたい.
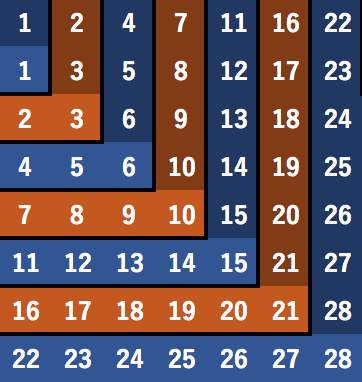
ちょっと考えると, $S_1=\{1,\underline{2}\},S_2=\{1,\underline{3}\},S_3=\{\underline{2},\underline{3}\}$のように, 要素$2,3$を追加すれば良いと分かる.
この$S_1,S_2,S_3$と共通成分を1つずつもつような$S_4$を作りたい.
同様にして, $S_1=\{1,2,\underline{4}\},S_2=\{1,3,\underline{5}\},S_3=\{2,3,\underline{6}\},S_4=\{\underline{4},\underline{5},\underline{6}\}$のように, 要素$4,5,6$を追加すれば良い.
こんな感じで再帰的に構築できそうだという予想がつく.
このとき, $\displaystyle N = 1+2+\cdots+k=\frac{k(k+1)}{2}$より, 三角数でなければならない.
提出コード(Python3🐍)
n = int(input())
r = int((n * 2) ** .5)
if r * (r + 1) != n * 2:
print('No')
exit()
# nは三角数
res = [[] for i in range(r + 1)]
tmp = 0
for i in range(r - 1):
for k in range(tmp, r - i + tmp):
res[i].append(k + 1)
res[i + k - tmp + 1].append(k + 1)
tmp += r - i
res[-2].append(n)
res[-1].append(n)
print('Yes')
print(len(res))
for l in res:
print(len(l), *l)